El teorema de pitágoras
Explicación
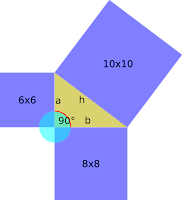
Este teorema dice algo así: "En un triángulo rectángulo, la suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa"... ¡Valla! si esto lo hubiera sabido antes y pensar que es tan fácil de entenderlo pero los maestros siempre me ponían cosas así "a²+b²=h²" o "h=√a²+b²".
Se expone este tema por cuatro razones específicas, la primera es para cubrir una necesidad de incluir problemas de enseñanza de una manera práctica, la segunda es para extender un poco los temas tratados en este blog, la tercera es para exponer un proceso que hemos empleado en los procesos expuestos en este blog y la cuarta se expondrá al final del artículo.
Se expone este tema por cuatro razones específicas, la primera es para cubrir una necesidad de incluir problemas de enseñanza de una manera práctica, la segunda es para extender un poco los temas tratados en este blog, la tercera es para exponer un proceso que hemos empleado en los procesos expuestos en este blog y la cuarta se expondrá al final del artículo.
Conceptos previos
Se conoce como Hipotenusa a la linea contraria al ángulo recto (90° grados) en una figura triangular.
Se conoce como cateto a las lineas que llegan hasta el ángulo recto de un triángulo rectángulo.
Antes
Tenemos un planteamiento donde se nos pide calcular la distancia de una banqueta en un terreno que fue cortado en diagonal para hacer una vialidad pero desconocemos cuantos metros hay que cubrir si los terrenos en esa zona son de 8X6.
Durante
Entonces ya con estos datos procedemos a calcular la distancia de la banqueta teniendo que por lo regular los terrenos son rectángulos y por consiguiente la esquina del terreno opuesta a la banqueta es el ángulo recto determinamos que la operación mas simple para realizar esta es mediante el teorema de pitágoras.
Después
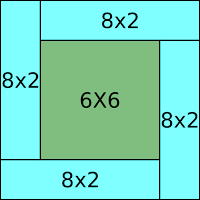
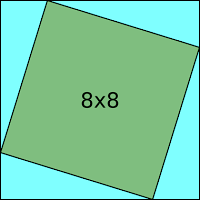En el caso de los terrenos no siempre se requiere una comprobación, pero en muchos casos si, como la mayoría de la enseñanza es más entendida de manera visual ademas que este presenta características didácticas para los alumnos la demostración anterior es la mas empleada, sin embargo por gusto propio y para no extender este tema demasiado yo prefiero la otra comprobación, que como gusto mas de las operaciones matemáticas es mucho mas sencillo de comprobar.Ejemplo
- a²+b²=h² | 6²+8²=?² | (6x6)+(8x8)=(?x?) | 36+64=(?x?) | 100=(?x?) | 100=(10x10) | 100=100
- h=√a²+b² | h=√6²+8² | h=√(6x6)+(8x8) | h=√36+64 | h=√100 | h=10
Como vemos en estos ejemplos aplicados a las primeras fórmulas que se presentaron al inicio de este artículo, sin embargo en el segundo la hipotenusa está despejada, es decir dejándola sola en uno de los lados de la igualdad.
- ¡uy, pero que aburrido eres! ¿no tendrás un ejemplo mas acorde con mi edad?
- Veamos ... ¡Ya se!
Supongamos una tirolesa que está a 7 metros de altura y tiene que recorrer 25 metros de largo hasta la llegada, la pregunta es ¿cual es tamaño de cable en todo el recorrido?
Entonces tendríamos cable = √(7x7)+(25x25) | √49+625 | √674 | 25.96, es decir cable de 25.96 mts.
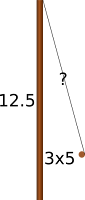
O ¿cuanto de largo hay en una tela para hacer las velas de un velero (de esos que coleccionaras cuando seas mayor) que en su mástil tiene una altura de 12.5 mts. con una cruz a 5 metros de altura de la cubierta y 3 mts. separado del mástil?.
Entonces tendríamos largo = √((12.5 - 5) x (12.5 - 5))+(3x3) | √(7.5x7.5)+(3x3) | √56.25+9 | √65.25 | 8.07, es decir el largo de una vela sería de 8.07 mts.
O Hacer una resbaladilla de 1.78 metros de altura y que llegue a 3.6 metros de largo y ...
- Está bien, ¡ya entendí!, el teorema de pitágoras sirve para muchas cosas divertidas también, de hecho te entendí desde lo de la tirolesa.
- ¡uy, pero que aburrido eres! ¿no tendrás un ejemplo mas acorde con mi edad?- Veamos ... ¡Ya se!
Supongamos una tirolesa que está a 7 metros de altura y tiene que recorrer 25 metros de largo hasta la llegada, la pregunta es ¿cual es tamaño de cable en todo el recorrido?
Entonces tendríamos cable = √(7x7)+(25x25) | √49+625 | √674 | 25.96, es decir cable de 25.96 mts.
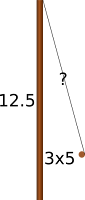
O ¿cuanto de largo hay en una tela para hacer las velas de un velero (de esos que coleccionaras cuando seas mayor) que en su mástil tiene una altura de 12.5 mts. con una cruz a 5 metros de altura de la cubierta y 3 mts. separado del mástil?.Entonces tendríamos largo = √((12.5 - 5) x (12.5 - 5))+(3x3) | √(7.5x7.5)+(3x3) | √56.25+9 | √65.25 | 8.07, es decir el largo de una vela sería de 8.07 mts.
O Hacer una resbaladilla de 1.78 metros de altura y que llegue a 3.6 metros de largo y ...
- Está bien, ¡ya entendí!, el teorema de pitágoras sirve para muchas cosas divertidas también, de hecho te entendí desde lo de la tirolesa.
Herramientas recomendadas
Evaluación
¿Que es la hipotenusa?¿Que es un triángulo rectángulo?
¿Que son los catetos?
Ligas internas
Ligas externas
 | |||||||
| Vea COMPLETO el Teorema de Pitágoras (El Arte de la Lógica nº 2) Edición Kindle | En este caso es un libro electrónico gratuito para fomentar mas la lectura :D |
Algunos juguetes para apoyar esto de forma didáctica y fomentar su utilización y aplicaciones de manera divertida.
Incluso encontramos videos musicales de YT
Consejo
Conclusión
Y la cuarta razón es por SEO para acrecentar las vistas del blog, viendo que el concepto "teorema de pitagoras" como palabra clave tiene mas de 301,000 búsquedas al mes y hay poco mas de 346,000 páginas que responden a esta tentativa de búsqueda tenemos a rededor de 86.99% de probabilidades de que una parte de esas búsquedas nos encuentren a nosotros, al día de hoy tenemos 1,149 vistas en promedio al mes al dí 15 de septiembre de 2019, en 15 días veremos como ha funcionado, a un mes y a un año.
Comparamos la wikipedia como principal competencia sobre el tema y nuestra entrada propia para ver si algo nos interesa y que deberiamos incluir dentro de nuestra propia entrada, siendo el color verde lo comprendido dentro de nuestra publicación y el café lo que podríamos encontrar en la mayor competencia.
No hay comentarios.:
Publicar un comentario